Category Theory
Update 2023/4/4
YouTube
https://www.youtube.com/playlist?list=PLbgaMIhjbmEnaH_LTkxLI7FMa2HsnawM_
B站
https://www.bilibili.com/video/BV1Zf4y1L7bw
PDF: Category Theory for Progammers
Seattle, Summer 2016
FYI:
markdown里写KaTeX,用两个$号包裹住数学代码就好了,中间的符号参考 (如果用一个$ 目前Docusaurus有些问题)
如:
$$
h \circ (g \circ f) = (h \circ g) \circ f
$$
https://katex.org/docs/supported.html
LaTeX: https://en.wikibooks.org/wiki/LaTeX/Mathematics#Multiplication_of_two_numbers
基本上KaTeX 和LaTeX在and or 有区别(前者是land 和lor),然后\C这些不支持
一些特殊集合符号:
https://texblog.org/2007/08/27/number-sets-prime-natural-integer-rational-real-and-complex-in-latex/
Stackexchange Mathematics
https://math.stackexchange.com/
Motivation and Philosophy
大佬讲了自己的很多历程,一开始写汇编,然后又转到C++,写Template。后来又转到Haskell
人类解决复杂问题的办法,通常都是把问题切成小的,可以解决的问题,再将结论合并起来。"Compose and Decompose"。各种问题都是如此,包括物理学(弦理论)等等,都是这样去做的。
当然,这种无限切分只是一种思想的方式,可能是人类在进化过程中得到的独特的能力,并不一定是自然的内在属性。所以Category Theory 范畴论就是研究人类思维方式,而不是研究自然(物理、数学)的学科。
为什么需要结构?
"We need structure not because well-structured programs are pleasant to look at, but because otherwise our brains can’t process them efficiently."
"We can only keep 7 ± 2 “chunks” of information in our minds."
我们需要代码有结构,并且会对代码“整洁”与否进行判断,是因为复杂、混乱无结构的代码我们作为人类是很难处理的。
为什么强类型更好,单元测试不能代替类型判断吗?
Testing is a poor substitute for proof.
数学上的证明是严谨的,而单元测试却并非一个决定性(Deterministic)的过程,而只是一个概率性的过程(Probabilistic)。而且,如果在一个弱类型的语言,修复UT就更加难(如果大范围修改类型的话),因为对弱类型这些“类型”本质上都是同一类型的不同同构,因此问题会更隐蔽。
计算需要时间
f :: Bool -> Bool
这个函数返回值有几种可能性?True, False?
事实上,还有(bottom)。这个bottom就代表这个程序永远没有返回值。
在Haskell中,bottom是任何类型的元素(如果把每一种类型视为其所有可能值的集合)
同时,这种可能返回函数也被称为partial function
为什么需要数学模型?
That means we do reason about programs we write, and we usually do it by running an interpreter in our heads. It’s just really hard to keep track of all the variables. Computers are good at running programs — humans are not!
还是一样,因为人太容易犯错了。目前码农们写代码的方式,就是尝试让自己变成一个人肉编译器——先想好逻辑,再实现。但是正是这个过程引入了很多问题。因此,我们要让代码能够用上数学的证明,这就要求每个编程的概念都和数学的表示关联。(denotational semantics(指称语义))
比如在Haskell中的数组元素相乘:
fact n = product [1..n]
而在很多程序中,我们不得不写循环来实现。
What is a Category?
人类的思想武器库里,有三把利器:
Abstraction, Composition 和Identity
所谓抽象,就是get rid of the details(减少不必要的细节)。
而Composition,在上一讲已经提到,就是人类特有的将问题的解答组合的能力。
Identity,指的是分辨两个事物是否相同(Identical),这个很重要,像HoTT就是研究这方面的内容的。
那么,Category该怎么定义呢?
Milewski教授说,Category就是“a bunch of objects”,一堆事物。Object在范畴学里是一种Primitive(原始的)概念,没有任何属性,类似物理里的“点”。为什么不说是a set of objects呢?我们都知道,Set(集合)在数学里是有特殊含义的。最基本的定义,就是判定一个集合包含哪些元素,或者一个元素是否属于一个集合,这个叫Membership。Membership通常是由一条自然语言的规则制定的,因此常常会出现矛盾,比如著名的罗素悖论(理发师悖论)。
此外,我们还有Morphism(态射),指两种状态之间的一种映射关系。
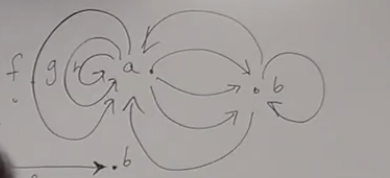
元素之间的映射可能有很多种,可能有无限种。
对于元素的组合,比如,那么可以说
在这里,和是等价的,这就是Composition(组合)。
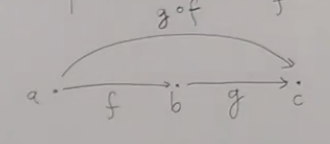
值得注意的是,如果和这两个态射存在,是必然存在的。
那么,这个概念就很好理解了:
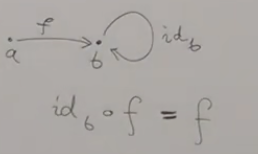
这就是一个指向自身的态射,如.既然每种组合都必然存在,那么也必然存在,且,是不是很像这个概念呢?
注意,这里并没有“交换律”(Commutative property),即便是,和也是不同的!(当然结果可能是相同的,但从定义来说是不同的)
Associativity(结合律)
有同学提问:和群的区别在哪?
群(Group)的概念,我们可以看到,有四种:
Closure(封闭性,当然这并不是必要的,二元运算就已经满足了这个公理)
Associativity(结合律)
Identity Element(有单位元素)
Inverse Element(有反元素)
交换律是不一定成立的,满足交换律的群称为阿贝尔群(Abelian group)
我们可以列一张表:
| 结合律 | 单位元素 | 反元素 | 交换律 | |
|---|---|---|---|---|
| 群 | √ | √ | √ | |
| 半群 | √ | |||
| 独异点(Monoid) | √ | √ | ||
| 范畴(Category) | √ | √ | ||
| 阿贝尔群 | √ | √ | √ | √ |
从这个角度上说,范畴和独异点(也称为幺半群)很相似。事实上,范畴的概念本身,就是对幺半群的延伸。
在Haskell、ML中,这些object就是Type,而morphism就是函数。
那么什么是Type呢?Type可以认为是A set of values,(当然也可能是空集),而Category 做的就是把这些Sets看作Object,进行了更高维度的抽象。
Functions, epimorphisms
什么是Pure function(纯函数)?
所谓纯函数,就是给定相同(Identical)的参数,得到的返回值也是相同(Identical)的。
那么,我们可以把集合之间的Morphisms态射看作纯函数吗?
比如,isChar函数,就是用了查表,将所有的结果都存储下来,用的时候直接查。事实上,任何一个从同一类型转为另一类型的纯函数,我们都可以将它们的结果转化为一张结果表。当然,之所以我们不能这么做,因为集合的大小可以是无限的,表的大小也是无限的,而现实的资源确实有限的。
可以思考一下,random()是纯函数吗?
Cartesian Product
表示为(叉乘),数据库里full join就是这个笛卡尔积。按照定义,任何一个笛卡尔积的子集,都是关系(Relationship)。关系是没有方向的,而Function是有向的。比如对关系而言,中的某个元素a可以与任意多个中的元素有关系,而反之亦然。
如果函数f的起点作用域是,终点作用域是,那么:就是Domain(定义域),就是Codomain(对应域),而真正产生值的落点组成的集合为Image(值域)。
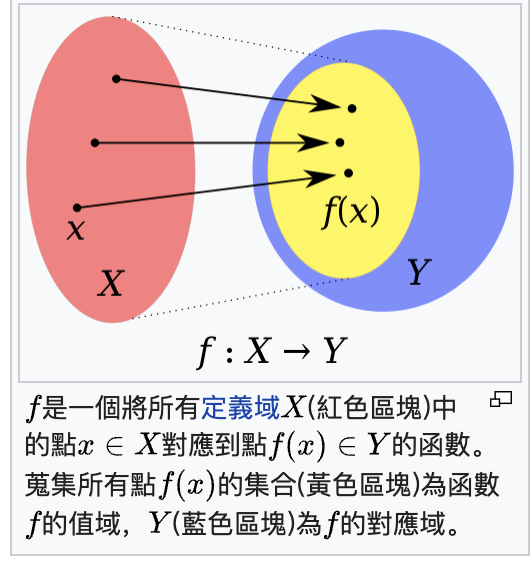
我们高中的时候就学过,什么样的函数称为可逆函数:函数的定义域(Domain)和值域(Image)是一一对应的关系。如果两个函数的转换满足:
那么称这两个函数中任意一个函数为同构(Isomorphism)
绝大多数的函数都不是同构。
而对于这些不是同构的函数,比如:isEven,我们其实是做了进一步的抽象,扔掉了许多信息,只剩下一个boolean。
单射 Injection 就是没有扔掉任何信息的函数
如果Image和Codomain是相同的,那么函数就是Surjective(满射)
Injective & Surjective 就是Bijection(双射)
那么,Bijection和Isomorphism有啥关系吗?傻傻分不清楚。
可以看到,Isomorphism is a structure preserving bijection.
对范畴论来说,Injection使用另一个词,就是Monomorphism(单同态)
而Surjective就是Epimorphism(满同态)
假设对于一个Category 中,有和,以及从到的态射
那么,是满同态的充要条件是:
Monomorphism, simple types
是单同态的充要条件是:
Types
对应void
这里有一个非常非常有意思的东西:
:: void -> int 存在吗?
我们可以根据定义:任何一个态射,都是定义域和对应域的笛卡尔积中的一个子集。既然
中,为,那么。
然后,由于空集的定义:空集包含于所有集合
所以空集也包含于空集
因此我们构造态射的条件满足了:这个子集就是,对于
Milewski大佬的比喻很形象:这个Void -> Int函数就很像是一个”吹牛“函数:只要输入者提供一个Void类型的参数,那么它就能返回一个Int类型。由于输入者永远也无法在调用时输入一个Void类型的参数,因此这个函数不仅成立,而且永远无法被成功地调用!
事实上,这个函数就是Haskell中的Data.Void中的absurd 函数:
absurd :: Void -> a
然后还有更加有意思的一件事,即:既然用Void作为参数,函数永远无法被真正使用,因此Void -> Void也是存在的。
当然,如果是A -> Void就不存在了,因为对于任意一个元素i∈A,不存在b∈B(B=$ \varnothing$), 即不存在这样的态射f。
也就是说,absurd的反函数drusba是不存在的。
再来看看Haskell中的(),一般读作Unit
❯ ghci
GHCi, version 8.10.7: https://www.haskell.org/ghc/ :? for help
Prelude> :t ()
() :: ()
() 的类型……是…… ()
其实Type ()更像是一个抽象的概念,即一个只包含一个元素的集合(相比之下Boolean包含两个元素)。
如果定义一个函数 a :: () -> int
那么,可以思考一下:如果要满足Pure Function的概念,那么这个返回的Int也必须是固定的,因此是常值函数。
在C++中,我们会用一些返回“void”的函数,但这些函数返回的其实是一个具有部分功能的Unit,即()。
class unit_type {};
const unit_type the_unit;
unit_type f(unit_type) { return the_unit; }
unit_type g(unit_type) { return the_unit; }
int main()
{
f(g(the_unit));
return 0;
}
而Haskell中的Void才是真正和 对应
C语言中的 function()和function(void)
http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1570.pdf
T foo( void ); // declaration, foo takes no parameters
T bar(); // declaration, bar takes an *unspecified* number of parameters
T foo( void ) { ... } // definition, foo takes no parameters
T bar() { ... } // definition, bar takes no parameters
Examples of categories, orders, monoids
还记得Category的定义吗?Category就是A collection of "objects" that are linked by "arrows". 也就是说,对Category c中的任意object a, 其必然有identity morphism(单位态射),也叫自反性(Reflexivity)并且该范畴中任意态射都满足结合律。
因此,一个没有任何object的范畴存在吗?是可以存在的,因为两句任意开头的话都是真。
同样,一个只包含一个object的范畴也是存在的。
我们可以发现,Category在某些方面和图很像。事实上,图不总是范畴,但总可以通过添加arrow来使得图成为范畴。
Preorder(预序,先序) vs Total order
对于一个集合P,如果它的一个子集满足某种运算(比如≤),这就是preorder。
这个运算要满足Reflexivity(因为一个object必须存在单位态射才能存在于范畴中),而且还具备Transitivity(传递性),即
每两个object之间通向只存在一个态射,也可以不存在或者同时存在反方向的态射。
Partial order是Preorder中的一个特例,即它必须是DAG,两个元素之间没有反方向的态射。
而Total order中,任意两个object之间都有态射(都可作规则下的比较)
Hom-set
hom-set 就是 homomorphism set 的简写,在范畴论中,同态就是态射,因此hom-set就是一个个二元素集合(包含每个态射的起点和终点)
Thin / Thick Category
- “Thin” (Posetal category) 每两个object之间只有一个态射
- “Thick” thin之外的情况
Monoid
独异点的概念在范畴论之前就出现了,它满足单位元素,结合律。
几个经典的例子,比如乘法,加法
字符串拼接也是,比如空字符串""就是独异点。当然,这个例子比较特殊,因为这恰好说明了Monoid本身的规则并不一定满足交换律,因为字符串拼接显然不满足交换律。
那么,在范畴论中,Monoid指的就是只有一个object的范畴,其Hom-set就是M(a, a)
Monoid在程序中对应着Weak Typing(弱类型),即所有的function都能调用另一个function(当然这里的function依然是Pure function的概念),弱类型的类型间可以相互转化,事实上从抽象的角度来说它们都属于同一种类型。
注意:这里的一个object,指的不是一个element!object在这里指一种抽象的类型。
Kleisli category
Kleisli category涉及到monad的一些知识,后面会讲(挖坑),但是可以先简单直观地用一个例子来理解。
我们都知道,Pure function对相同的输入总是返回相同的结果,并且没有任何Side effect(隐藏的dependency)
假设有一个非常trivial的函数:
bool Not(bool x) {
return !x;
}
假设要在这个函数里加上一个打日志的操作,那么势必是对缓冲区中某个字符串做了修改:
// unknown area
string buffer = "xxx";
// ......
bool Not(bool x) {
buffer += "Called Not";
return !x;
}
这个函数显然是不符合纯函数的定义的。那么,要怎么修改呢?唯一的办法,就是把buffer从隐藏的依赖(side effect),变为显式的依赖(parameter)。并且,这个修改buffer的结果也同样不能用隐藏的方式传出去,而是用返回的形式。
pair<bool, string> Not(bool x, string buffer) {
buffer += "Called Not";
return make_pair<bool, string>(!x, buffer);
}
上面的代码其实违背了Separation of concerns(分离原则),即对于string buffer而言,它的内容与Not这个函数无关,Not所做的仅仅是将"Called Not"附加在buffer后返回。因此,原buffer的内容是Not完全用不到的。
经过修改,我们可以得到:
pair<bool, string> Not(bool x) {
return make_pair<bool, string>(!x, "Called Not");
}
但是,有一个问题在于:谁负责真正地去做string append的操作?而且,也不难发现,Not的入参和出参并不匹配。原本的Not可以调用自己的结果(Composition),而现在却不行了。
因此,我们需要额外加一个Composer:
template<class A, class B, class C>
function<pair<B,C>(A)> compose(function<pair<A, C>(A) f, function<pair<B, C>(B) g)
{
return [f, g](A x){
auto r1 = f(x);
auto r2 = g(r1.first);
return make_pair(r2.first, r1.second + r2.second);
}
}
这其中C可以是string
C++14中,还可以用
auto const compose = [](auto f, auto g){
return [f, g](A x){
auto r1 = f(x);
auto r2 = g(r1.first);
return make_pair(r2.first, r1.second + r2.second);
}
}
我们已经定义了Composition(组合),然后定义Identity:
template<class A> A identity(A x) {
return make_pair(x, "");
}
并且,字符串的结合是符合结合律(Associativity)的。
Terminal and Initial objects
在范畴论中,Initial Object(初始对象)和Terminal/Final Object(终结对象)的定义如下:
对一个范畴C中的Object I, 如果对任意C中的对象A,都有且只有一个从I到A的态射,那么I就是初始对象。而如果对任意C中的对象A,都有且只有一个从A到I的态射,那么就说I是终结对象。
由此,我们也可以推出,任意两个初始对象都是同构(Isomorphic)的。
其实这个概念,可以理解为一个范畴中“最小”和“最大”的元素。显然,在偏序关系的范畴中,是不存在初始和终结对象的。
在一个集合范畴(Category of sets, 或Sets)中,显然$ \varnothing$是初始对象。还记得我们之前提到的absurd函数吗?那个从Void指向任何类型的函数,有且只有一个。
而终结对象,则是一个单元素集合(Singleton set),因为从任何一个对象指向单元素集合,都只能有一种态射,即常值态射。
那么,为什么初始对象不能是单元素集合/其他集合呢?因为我们是在集合范畴的语境下讨论的。如果是其他的范畴,比如非空集合的范畴,那么初始对象就是单元素集合了。
范畴中可能没有初始对象,也可能没有终结对象。
如果初始对象和终结对象相同,那么其称为零元素。
Duality
opposite category (对偶范畴)
对任意一个范畴C,我们都能定义一个和它对偶的范畴,其中所有的箭头都是相反的,而C的起始、终止对象分别是的终止、起始对象
Product
我们也许都知道,Cartesian product(笛卡尔积)就是两个集合的元素一一组合的二元对组成的集合。
如果将笛卡尔积也定义为一个对象,从笛卡尔积出发,那么就有两个分别指向原始两个集合的态射:
First() 和 Second()
First :: (a, b) -> a
Second :: (a, b) -> b
那么,如何证明原来的笛卡尔积是最合适的笛卡尔积呢?
假设,用Int作为 Int 和 Bool的笛卡尔积:
p :: Int -> Int
p x = x
q :: Int -> Bool
q _ = True
当然,也可以用三元组,如(Int, Int, Bool)来作为笛卡尔积
p :: (Int, Int, Bool)
p (x, , ) = x
q :: (Int, Int, Bool)
q (, , b) = b
p' = p . m
q' = q . m
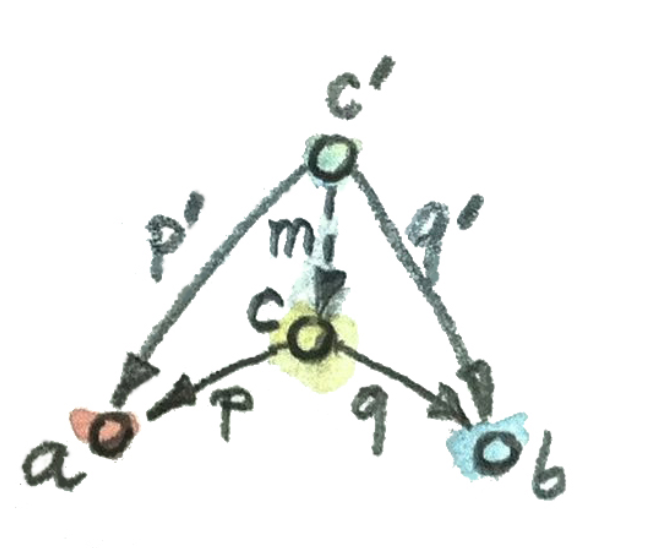
第一种构造,不是满射(, False)的情况没有包含,缺少了信息
第二种构造,不是单射,从(x, x, y) 到(x, y) 包含了两种可能性,引入了歧义。
因此,只有一种笛卡尔积,那就是正好是(Int, Bool)
Coproduct
Coproduct
如果我们把前面一小节的图每个箭头都反着画,就得到了Coproduct.
可以看一下拓扑中的不相交并概念:
也就是说,这个Coproduct就是A或B,但是是不相交并,即Either的关系
data Either a b = Left a | Right b
让人想起Typescript中的
let a: string | number
但是我们也知道,一旦a的类型是 string | number,后续所有对a的操作都需要进行类型判断。
Asymmetry
Functions大多是不对称的,即不能像求对偶范畴那样把所有箭头倒过来
事实上,Set(Category of sets)就是没有对偶范畴的。可以存在从 到其他对象的态射,且对每个对象都只有一条(正因如此, 是Set的初始对象)。然而,却不能反着从非空的集合对象构造态射到 ,因为无意义。
Algebraic data types
Product types
product在编程语言中对应的概念就是元组(Tuples),在Cpp中就是Pair。
Pair中的元素显然不能交换位置:(a, b) 和 (b, a)是不一样的类型。
swap :: (a, b) -> (b, a)
swap (x, y) = (y, x)
但是,这样的元组其实是携带了同样的信息的,只是编码的方式不同。因此,在范畴论的概念中,由swap函数就可以实现他们之间的同构。
同样的,嵌套Tuple也是如此:
alpha :: ((a, b), c) -> (a, (b, c))
alpha ((x, y), z) = (x, (y, z))
这一次不再是同一个函数,但也依然是Isomorphic的
下面,我们可以看一些很有意思的:
(a, ())
这个(a, ()) 和 a 是同构的,原因就在于Unit () 本身是不携带任何信息的。
rho :: (a, ()) -> a
rho (x, ()) = x
rho_inv :: a -> (a, ())
rho_inv x = (x, ())
我们可以随便构造从Tuple中取走Unit,或者加上Unit的函数,而不需要额外的信息或者省去信息。()本身不携带任何信息
Sum Types
Either本身是具有交换律(Commutative)的,很好理解:
data Either a b = Left a | Right b
data Either a b = Right b | Left a
是没有区别的。
Algebra of Types
通过上面的例子,我们可以发现:Product和Coproduct可分别作为乘法和加法的近似,而Unit () 代表1,Void代表0
比如(a, Void) ~ Void
为什么呢?
因为
因为没有Void类型的实例,所以永远构造不出包含Void的Tuple,所以和Void是同构的。
同样,加法中有分配率(Distributive property)
(string, number | string) 和 (string, string) | (string, number)是等价的
从这个意义上说,乘法带着加法就是半环(Semiring), 由于无法定义减法,因此不是Ring(环)。有时半环也被称为Rig
Functors
函子 Functors
如何用Category表示集合?
任意object a都只有a->a的identity,没有其他的态射。称为Discrete category(离散范畴)
functor是在范畴之间的映射。如果给定两个范畴C和D,以及一个函子F,a是C中的一个对象,那么它在D中的image(像)就用Fa(无括号)表示。
对象可以映射,那么对象间的笛卡尔积(homset)自然也有映射
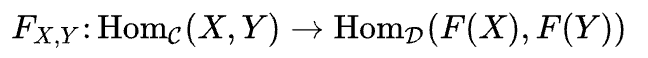
| Functor F | F X, Y |
|---|---|
| Faithful | Injective |
| Full | Surjective |
| Fully faithful | Bijective |
当然,除了对象,还有态射。
如在C中有一个态射f,从a->b:
f :: a->b
那么它在D中的像Ff,就是a的像指向b的像:
Ff :: Fa->Fb
对特征态射:
F id a = Id Fa
显然,由于对任意C中的f, g 都有其在D中的像Ff Fg
且 的映射
函子是一种保留结构的映射(Structure preserving)
什么是保留结构呢?就有点像人->火柴人
可以在保留结构的情况下,扩大/缩小,这个“结构”就是态射、对象的组合所表现出的特征
Endofunctor: 指向自身的Functor
Constant functor: Δ𝑐 , 最大限度地缩小范畴,即一个范畴被映射为另一个范畴中的对象, 则称次Functor为常量函子
Equational Reasoning
绝大多数情况下,两个Category之间的转换都是Functor(满足成为Functor的条件)。
functor事实上就是type constructor,获取一个type而生成另一个type。
class Functor f where
fmap :: (a->b)->(f a -> f b)
比如List:
data List a = Nil | Cons a (List a)
instance Functor List where
fmap _ Nil = Nil
fmap f (Cons x t) = Cons (f x) (fmap f t)
Reader functor:
比如:
private sealed class FuncReader<R, A> : IReader<R, A>
{
private readonly Func<R, A> func;
public FuncReader(Func<R, A> func)
{
this.func = func;
}
public A Run(R environment)
{
return func(environment);
}
}
这里的reader就用了reader functor的思想。
Functor可以被认为是容器(Container),比如List、Array,包括Reader可以看包含无穷序列的容器(如Int: [1..]) 而Maybe则和如C#中的Task,Cpp中的future对应。
Functoriality, bifunctors
: category of categories
所谓bifunctor, 其实和function很相似:
此时和的笛卡尔积(这三者都是范畴Category) 就是从C中任取对象和D中任取对象组合而成的二元组(c, d)形成的对象形成的范畴。
在haskell 中, f a b = (f a) b
比如:
instance Bifunctor (,) where
bimap f g (x, y) = (f x, g y)
bimap (+ 2) (++ "nie") (3, "john") --> (5,"johnnie")
bimap ceiling length (3.5 :: Double, "john" :: String) --> (4,4)
instance Bifunctor Either where
bimap f g (Left x) = Left (f x)
bimap f g (Right y) = Right (g y)
Monoidal Categories, Covariant Contravariant Functors, Profunctors
Monoidal Category我们之也记录了,就是满足有ID、结合律的单Object范畴。
functor非常好用,比如最常见的用法:
Gf ∷ (a -> b) -> (Ga -> Gb)
这里的Ga隐含了
Ga :: a -> r
也就是说,functor(实际就是Covariant Functor,因为其保留了箭头的方向)其实就是
Gf ∷ (a -> b) -> ((a -> r) -> (b -> r))
这里我们回到最简单的逻辑:
如果我有a->b,我想得到a->r。那么我会毫不犹豫地想,我要找到一个 b->r的函数,这样就可以把 a->b->r 通过结合律等价于a->r
但是,如果我有a->r,我想得到b->r呢?那么,我需要一个Prepend的函数,先把b->a。
因此,同样的式子反过来也是有意义的:
Gf ∷ (b -> a) -> ((a -> r) -> (b -> r))
因此这其实就是一个箭头从哪里开始指的问题。而上面这个functor,就是contravariant functor(逆变函子?)
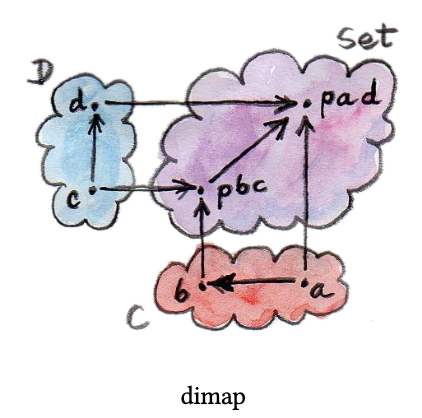
class Profunctor p **where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d dimap f g = lmap f . rmap g lmap :: (a -> b) -> p b c -> p a c lmap f = dimap f id rmap :: (b -> c) -> p a b -> p a c rmap =** dimap id
其实如果是
(a -> b) -> (d -> c) -> p b d -> p a c,是不是更好理解呢?因为这个和
(a -> b) -> (c -> d) -> p b d -> p a c 也同样都是在某种情况下成立的。
Function objects, exponentials
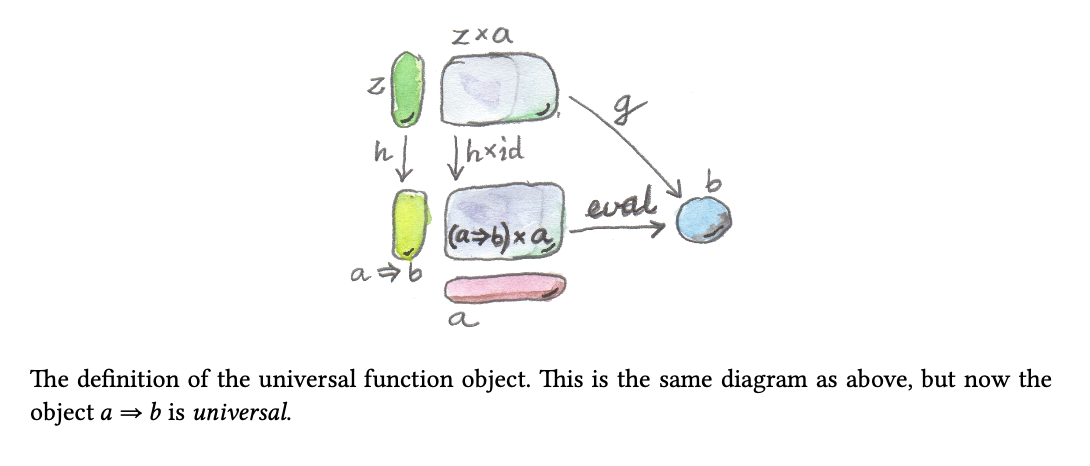
我们都知道,柯里化(Currying) 就是把函数从
变成
但是这个过程是如何做到的呢?
首先,对于
那么,我们之前已经证明过笛卡尔积的唯一性:,
那么,我们把这里的换成:
别忘了, 的最初定义
而 :
称为 的反柯里化
Cartesian Closed Categories
对任意一个Category,如果其满足以下几个条件,就称为Cartesian Closed Category:
1、有终止对象(Terminal Object)
2、任何对象间的笛卡尔积都在此范畴中
3、任何对象的幂(Exponential)
Exponential
代表Morphism的可能性总数
比如
就可以写作
即
(一个代表True返回的结果,一个代表False返回的结果)
Type Algebra, Curry-Howard Isomorphism
Curry-Howard-Lambek Isomorphism
proofs-as-programs and propositions- or formulae-as-types interpretation
| Object | 1 | 0 | And | Or | Implication |
|---|---|---|---|---|---|
| Logic | |||||
| Programming | |||||
| Category Theory |
可以看到,这几个概念都是互相一一对应的。最早是Curry-Howard Isomorphism,后来又延伸到了范畴学,因此叫Curry-Howard-Lambek Correspondence
Natural transformations
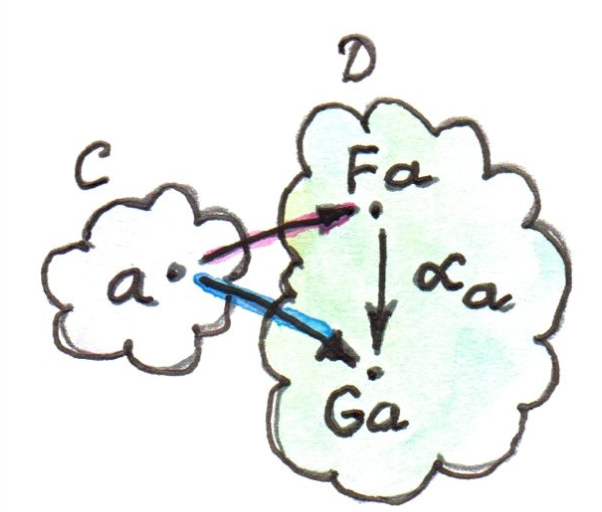
对任意两个Category 和 之间的两个Functor 和 ,如果
那么我们称这种态射为Component(分量)
如果对某些没有这样的态射,和之间就不存在自然变换。
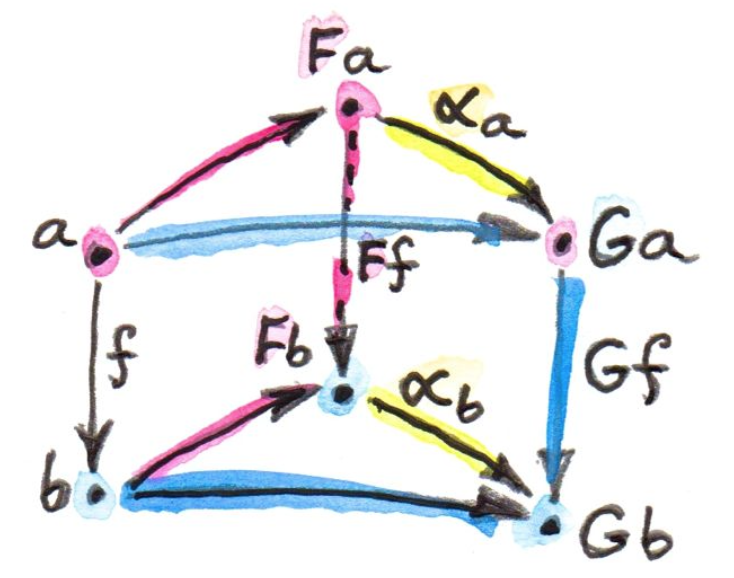
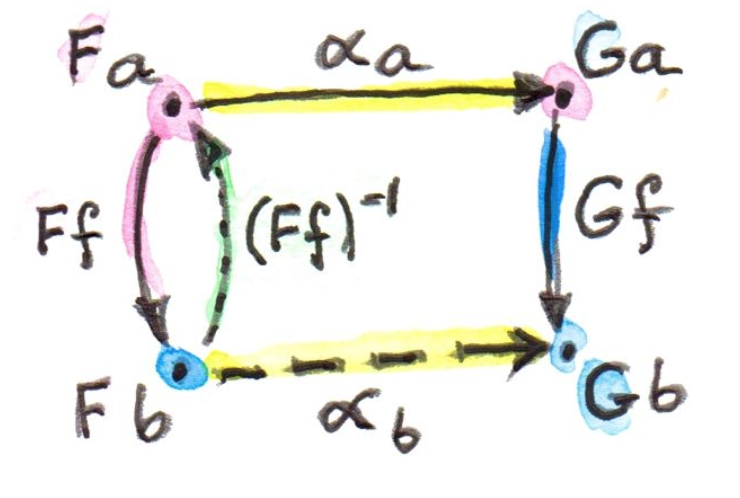
当然,除了对象之间的变换,我们自然也不能忘了态射。
要满足自然变换,对
都必须满足
同时,如果是可逆的,也必须满足
Count()
在编程中,最常见的Natural Transformation就是count/length了:
length :: [a] -> Int
这里看上去就是一个态射,但是它本质是。
我们可以假设
那么Count显然就是的一个态射了
Polymorphism
parametrically polymorphic function总是自然变换
Bartosz Milewski老师的书中说,Natural Transformation和多态有关系。我想这里还是要区分一下,确实和多态有关系,但并不是说多态就等同于Natural Transformation。比如我们都知道,像C++这些语言有泛型,假设这个函数本身是可以接受任意参数(比如容器vector等),并不是说这个函数接受了不同的参数后生成了不同的函数,而这些生成的函数之间有什么关系(这叫做ad-hoc polymorphism,即不同类型的逻辑还是不一定相同的,返回的类型也不一定相同)。
确切地说,这里的多态指的是参数parametric polymorphism多态,而parametric polymorphism则是构想了一个对通用的各种类型都适用的函数,而产生同样的结果。这里构造出的自然变换本质上源于
(参数)->(结果)->(结果的某种内禀属性)
之间的关系,比如Count 就是数组的一种内禀属性,这种属性在构造出"数组"这种类型的时候就必然存在。而从参数到这种内禀属性的关系,又蕴含在List(a)这个函数的逻辑中,这个逻辑可以是业务逻辑等等。
而更进一步说,类型本身是否也是一种函子呢?所有的类型都至少来源于初始对象Void
那么
是否也是自然变换呢?
2-Category, Bicategory
2-Category
那么,既然存在自然变换,套娃就开始了:
自然变换能不能也构成一个范畴呢?
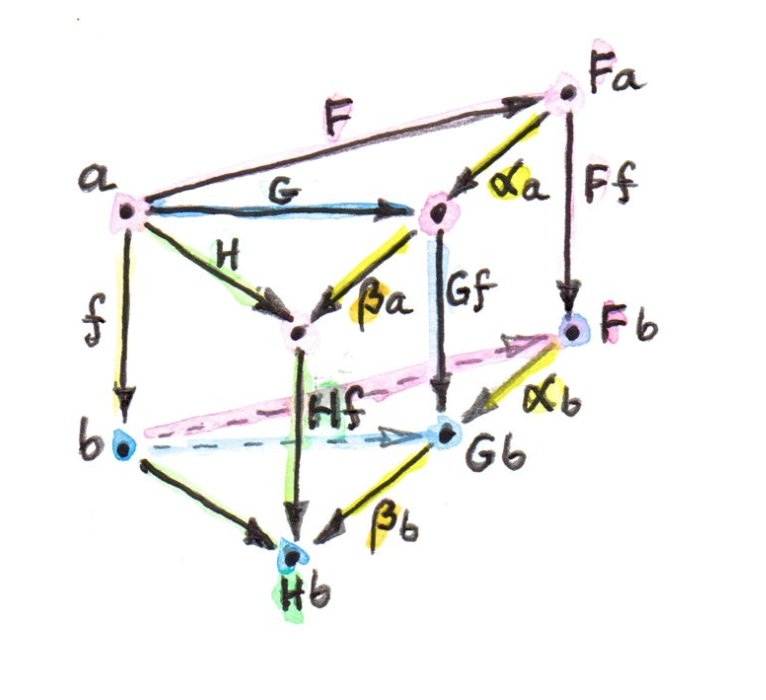
这个范畴中的对象就是Functors, 被写为
或 或
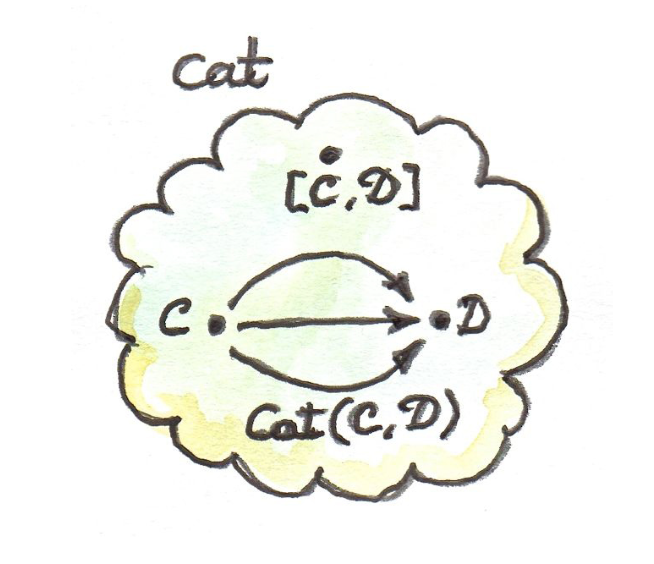
从这张小的插图可以看出,为何有时会写作了:Functor本身是具有方向性的
在其中,
0-cells (zero-cells) 指的就是object
1-cell 指的就是 morphisms between objects
2-cell 指的则是 morphisms between morphisms
这样的结构,就称为2-Category,具有两层嵌套结构。而用cell表示的方式称为CW complex(Cellular complex/cell complex)
它和Homset的区别在于,这个结构本身也是一个范畴,因此也是的一个成员。
Bicategory
又称为weak 2-category, relaxed 2-category,它弱化了范畴论中的定义,使得态射不必要满足严格的结合律/特征态射。
严格满足Associativity的2-category:
Up to isomorphism:
Span
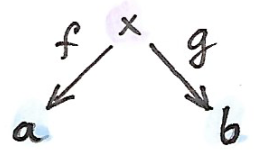
和之间的Span,就是一个外的对象以及分别指向和的态射和。
N-Category
既然有了2-Category,那么我们又可以定义3-Category, 4-Category …… 直到N-Category
Sets and Classes(?)
之所以又创造出Class这个概念,是数学家们为了规避罗素悖论的产物(NBG/MK from ZFC) 。简而言之,Class和Set都包含元素,但Set本身可以作为另一个Set/Class的元素,而Class则不行。(ZFC还没仔细研究过,不一定对)
参考:https://ncatlab.org/nlab/show/ZFC#constructive_versions
Large, Small and Locally Small
一个范畴如果其所包含的对象能够构成集合,那么这些对象就被称为small category(小范畴)。由于ZFC不允许Set of all sets的存在,因此实质上本身是不能构成Set的,或者它比Set更大,称其为large category。
一个范畴如果任意两个对象之间的态射都能构成集合,那么称其为Locally small。
Enriched Category
参考:https://bartoszmilewski.com/2017/05/13/enriched-categories/
Every category can be treated as enriched over Set, every 2-category can be considered enriched over Cat.
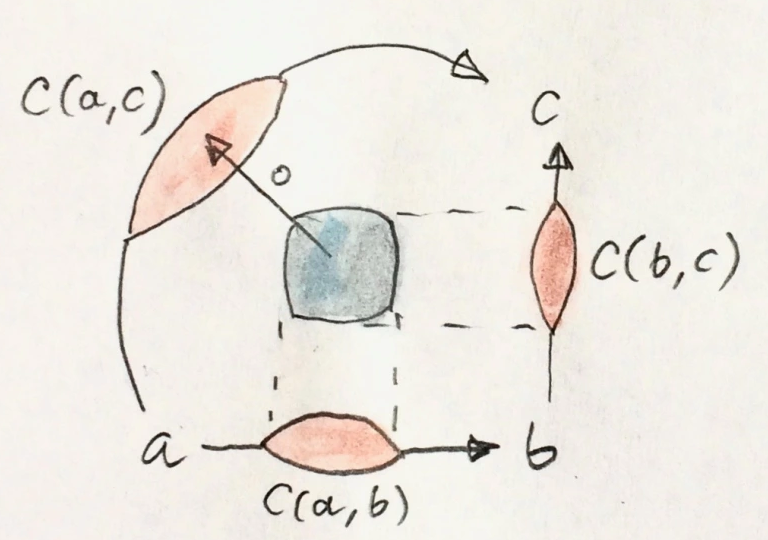
最开始我们对Morphism的定义为:集合和集合的笛卡尔积的子集
那么,我们也同样可以摆脱Set的束缚,将hom-set定义为hom-objects:
对每一个Morphism ,我们可以从中取一个对象。这个是一个普通的范畴,包含了中所有的对象对(因为我们没办法再看或者中的元素了,这个笛卡尔积本身也不存在态射了)
通过这种方式定义出的态射,也一样要满足结合律和传递性,即
显然(不是),这个是成立的,具体的证明过程在博客链接里有。
未完待续……